15 Columns
Introduction
Click to expand
Until now, our focus has been primarily on meeting strength and deflection criteria. While these aspects are crucial, it’s equally important to ensure the structure’s stability. In this chapter, we will delve into the stability analysis of long and slender members subjected to compressive loading, commonly referred to as columns. Some examples are shown in Figure 15.1. When the compressive load reaches a critical point, columns may undergo sudden sideways deflection, a phenomenon known as buckling. After buckling, a column is unable to support any further load. This chapter will focus on long, slender, homogeneous, axial compression members, otherwise known as columns.
In Section 15.1 we’ll derive the buckling formula for columns that are supported by pin connections at both ends. In Section 15.2 we’ll extend this to consider other common end conditions.
15.1 Euler’s Formula for Buckling
Click to expand
Even in ideal conditions, buckling often occurs for long slender members at loads significantly lower than the material’s crushing or compression limit. When a long slender object is subjected to axial loading, it may buckle once the load reaches a critical threshold known as the critical load, Pcr. At this point, the object experiences significant lateral deflection perpendicular to the load direction, so columns should be designed such that the applied load does not exceed the critical load.
Buckling of a ruler (long slender member) is depicted in Figure 15.2. The ruler in the left and center photos is subjected to axial load P that is less than the critical load, Pcr. This is known as stable equilibrium. In the photo on the right, the axial load, P, exceeded the critical load Pcr, causing a significant lateral deflection. This is known as unstable equilibrium.
15.1.1 Stability
We can consider stability by using a simplified model of a pinned-pinned column. This column will consist of two ridged bars connected with a pin and a spring with a stiffness k, as shown in Figure 15.3 (A). When the load, P, is small, the system remains vertical, and the spring is unstretched. If point C is displaced to the right a small amount, Δ, the spring will produce a force F = kΔ, as shown in Figure 15.3 (B). This force is used to resist the horizontal forces, Px = Ptanθ, as shown in Figure 15.3 (C).
Since θ is small:
\[ \sin \theta \sim \theta \text { and } \tan \theta \sim \theta \]
so
\[ \Delta=\theta \frac{L}{2} \text { and } 2 P_x=2 P \theta \]
Using the spring restoring force equation F=kΔ, then substituting in for Δ we have:
\[ F=k \theta \frac{L}{2} \]
If the spring restoring force is greater than the axial force, then we have a stable equilibrium.
\[ \begin{aligned} & F>P \\ & k \theta \frac{L}{2}>2 P \theta \end{aligned} \]
The θ cancels out, and we can solve for P:
\[ P<\frac{k L}{4} \]
Similarly we can solve for the expression for unstable equilibrium F < P:
\[ P>\frac{k L}{4} \]
The point at which F = P is crucial as it is the line between stable and unstable equilibrium. We call this the critical load Pcr:
\[ P_{c r}=\frac{k L}{4} \]
Thus, if the load P exceeds Pcr, then the system will be unstable, and if P is less than Pcr, then the system will be stable. We will use Pcr in the next section to determine the bucking load of columns.
15.1.2 Euler’s Formula
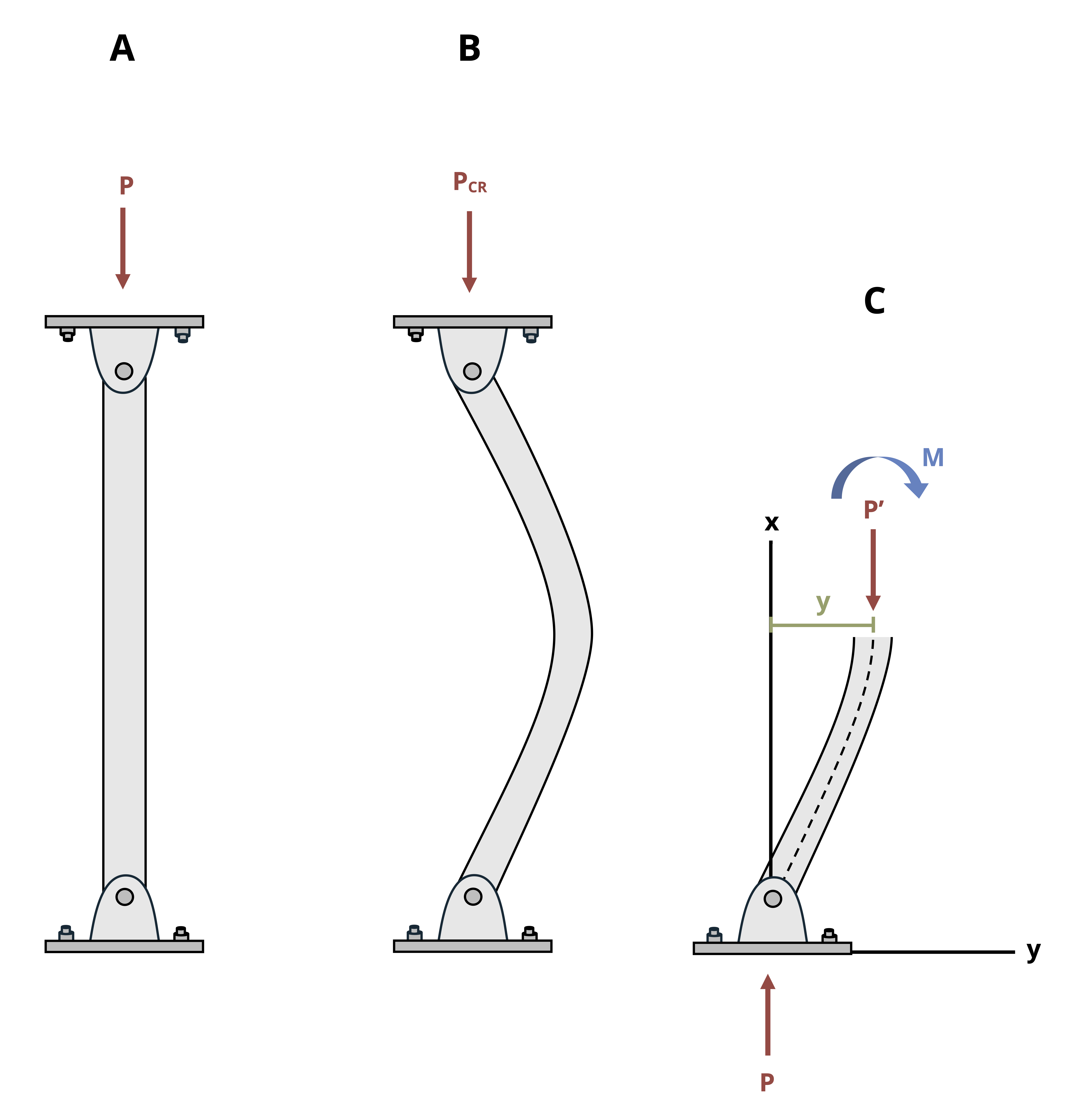
As mentioned in earlier sections, members can fail due to material yielding or fracturing. However, instability represents another critical failure mechanism that requires consideration. We will use Euler’s formula to calculate the theoretical buckling load. To do this, we will start with the simplest of columns, pinned-pinned end connections. This means that the column cannot translate but can rotate as shown in Figure 15.4.
Columns are similar to beams rotated 90 degrees, so we can use what we already know about the elastic curve.
\[ \frac{d^2 y}{d x^2}=\frac{M}{E I} \]
We can use the free-body diagram in Figure 15.4 (C) to sum moments about any point on the lower column section.
\[ \begin{aligned} & \sum M=0=M+P y \\ & M=-P y \end{aligned} \]
We can now substitute this expression into the elastic curve equation:
\[ \begin{aligned} & \frac{d^2 y}{d x^2}=\frac{-P y}{E I} \\ & \frac{d^2 y}{d x^2}+\left(\frac{P}{E I}\right) y=0 \end{aligned} \]
This is a linear, homogeneous, second-order differential equation with constant coefficients, which has a general solution of:
\[ y=C_1 \sin \left(\sqrt{\frac{P}{E I}} x\right)+C_2 \cos \left(\sqrt{\frac{P}{E I}} x\right) \]
The two constants, C1 and C2, can be determined by imploring boundary conditions. Since y = 0 at x = 0 and y = 0 when x = L. The first condition gives:
\[ \begin{aligned} &0 =C_1(0)+C_2(1) \\ & C_2 =0 \end{aligned} \]
The second boundary condition, x = L when y = 0 results in:
\[ 0=C_1 \sin \left(\sqrt{\frac{P}{E I}} x\right)+0 \]
The equation is satisfied if C1 = 0. However, this is a trivial solution that implies y = 0 and there is no lateral deflection. For the nontrivial solution, the sine function must be equal to zero, which requires:
\[ \begin{aligned} &\sqrt{\frac{P}{E I}} L=n \pi \\ & \text {where } n=1, 2, 3, 4,... \end{aligned} \]
The smallest value of P occurs when n = 1; substituting this and rearranging gives us Euler’s formula:
\[ \boxed{P_{c r}=\frac{\pi^2 E I}{L^2}} \tag{15.1}\]
where:
E = Elastic modulus of the material [Pa, psi]
I = Area moment of inertia for the column [m4, in.4]. Note if Ix and Iy are different, use the smaller value.
L = Unsupported length of the column (pinned=pinned connection) [m, in.]
This is named after the Swiss mathematician Leonhard Euler who developed this formula in 1744. Other bucking modes can exist (n = 2, n = 3, n = 4, etc.) but are less common as the load required for those higher modes would be much larger. The first three bucking loads can be seen in Figure 15.5.
15.1.3 Bucking Direction
Columns that are pinned at both ends and have circular or square cross sections (where the moments of inertia are the same about any axis) could buckle in any direction. However, columns that do not have a symmetric cross-section will take place in the plane perpendicular to the principal axis of the minimum moment of inertia. For example, the ruler in Figure 15.2 has a rectangular cross-section. When a compressive force is applied to the ruler, it will buckle about the axis with the smaller moment of inertia. The axis of bucking might not be obvious for sections that are not symmetric. During buckling analysis, it’s essential to evaluate both directions to determine the axis with the lowest moment of inertia. Subsequently, this axis is utilized for computing the critical buckling load. Figure 15.6 illustrates column buckling of wood supports.
15.1.4 Critical Stress
We can use the Euler bucking equation to calculate the critical stress for a column by setting I=Ar2 where A is the cross-sectional area and r is the radius of gyration. For a more comprehensive discussion on the radious of gyration, see the Engineering Statics book by Baker and Haynes.
\[ \sigma_{c r}=\frac{P_{c r}}{A}=\frac{\pi^2 E\left(A r^2\right)}{A L^2} \]
Rearranging we have:
\[ \boxed{\sigma_{c r}=\frac{\pi^2 E}{\left(\frac{L}{r}\right)^2}} \tag{15.2}\]
σcr = critical stress on the column just before it buckles [Pa, psi]. Note that this stress must be less than that of the yield stress, or the column will fail due to yield stress before it buckles.
E = Elastic modulus of the material [Pa, psi]
L = Unsupported length of the column (pinned=pinned connection) [m, in.]
r = Smallest radius of gyration of the column [m, in.]
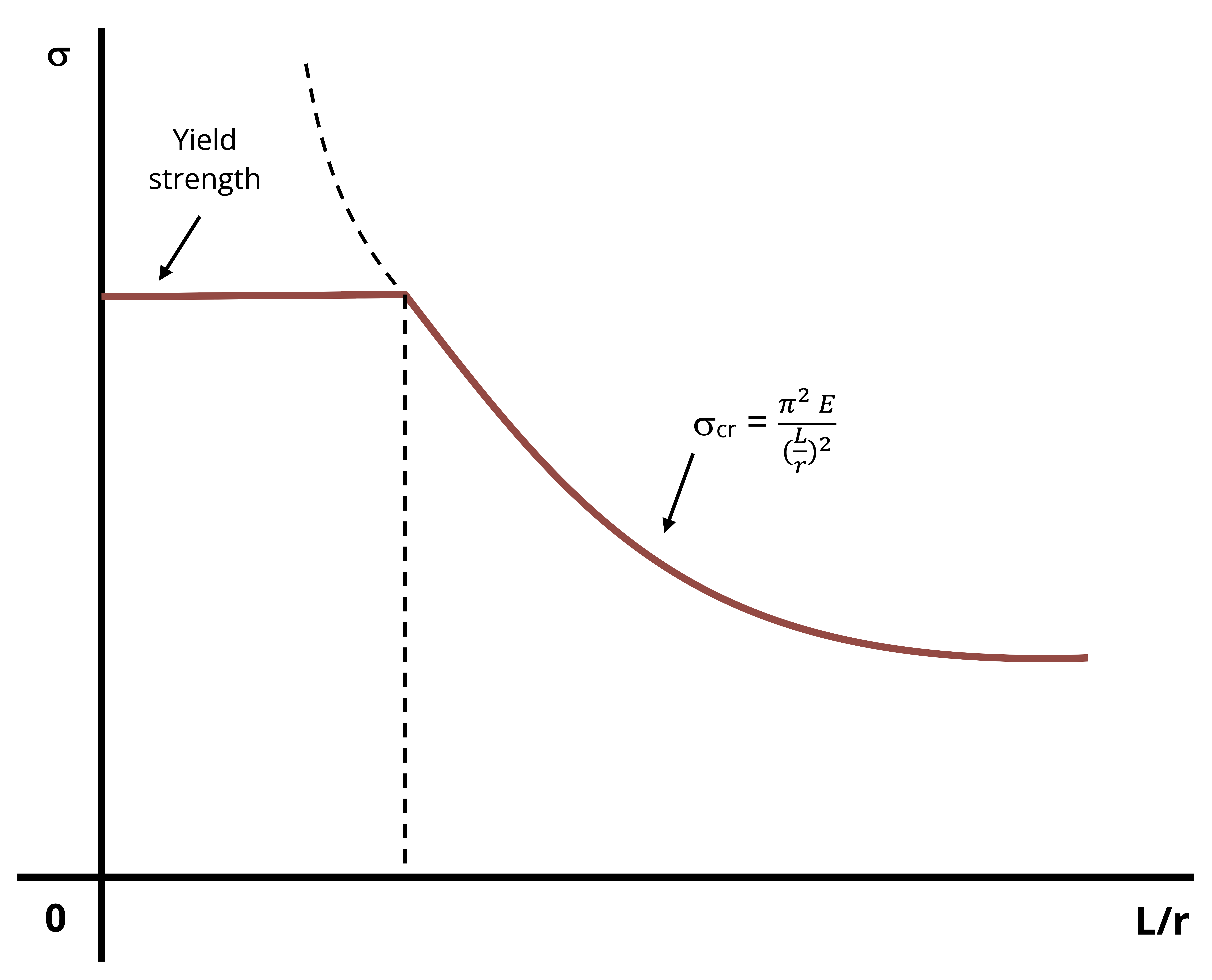
The quantity in the denominator, L/r, is called the slenderness ratio of the column. Many times columns are classified using the slenderness ratio as short, intermediate, and long. The smallest value of the radius of gyration is used to find the critical stress.
A plot of the critical stress versus the slenderness ratio is shown in Figure 15.7. For larger slenderness ratios the curve is hyperbolic. For smaller slenderness ratios, the critical stress is equal to the yield stress of the material. This graph illustrates that if the critical stress calculated using Euler’s equation is greater than the yield stress that is of no interest. The column will yield before it has the chance to buckle.
Example 15.1 demonstrates calculation of the critical buckling load and critical buckling stress.
Example 15.1
A pinned-pinned W10x30 column is 8 ft long made of A492 steel (σy = 50 ksi and E = 29,000 ksi) What is the largest load axial load that this column can support?
We will consult the table in Appendix A to get the section properties of a W10x30 section.
\[ \begin{aligned} & A=8.84{~in.}^2 \\ & I_x=170{~in.}^4 \\ & r_y=4.38{~in.} \\ & I_y=16.7{~in.}^4 \\ & r_y=1.37{~in.} \end{aligned} \]
We will start with calculating the critical load using Euler’s Bucking Formula. Note that we can confidently say that this column will buckle about the y-axis since the moment of inertia in the y-direction is the smallest.
\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I}{L^2}=\frac{\pi^2(29000{~ksi})(16.7{~in.}^4)}{\left(8{~ft}* 12\frac{in.}{ft}\right)^2} \\ & P_{cr}=518.6{~kips} \end{aligned} \]
This represents the load at which any increase in applied load will cause the column to buckle. We will calculate the stress associated with this critical load.
\[ \sigma_{c r}=\frac{P_{cr}}{A}=\frac{518.6{~kips}}{8.8{~in.^2}}=58.7{~ksi} \]
Since this stress is larger than the yield stress of the steel (σy = 50 ksi) the column will not buckle first. It will fail due to yielding. We can calculate the force using the stress of an axial member formula discussed in Chapter 2.
\[ \begin{aligned} &\sigma_{cr} =\frac{P}{A} \\ & 50{~ksi} =\frac{P}{8.84{~in.}^2} \\ &p =442{~kips} \end{aligned} \]
15.2 Effect of Supports
Click to expand
We derived Euler’s equation for bucking with pinned-pinned supports (the simplest case). However, in many cases, columns are supported by other end conditions. Just as we derived Euler’s formula for bucking by solving a differential equation for the pinned-pinned conditions, the same can be done for other types of support cases. We will derive one more here.
Let’s consider the case where a column is fixed at one end and free at the other end as shown in Figure 15.8 (A). Summing moments at the cut end of the free body diagram in Figure 15.8 (B) we get M=P(δ-y).
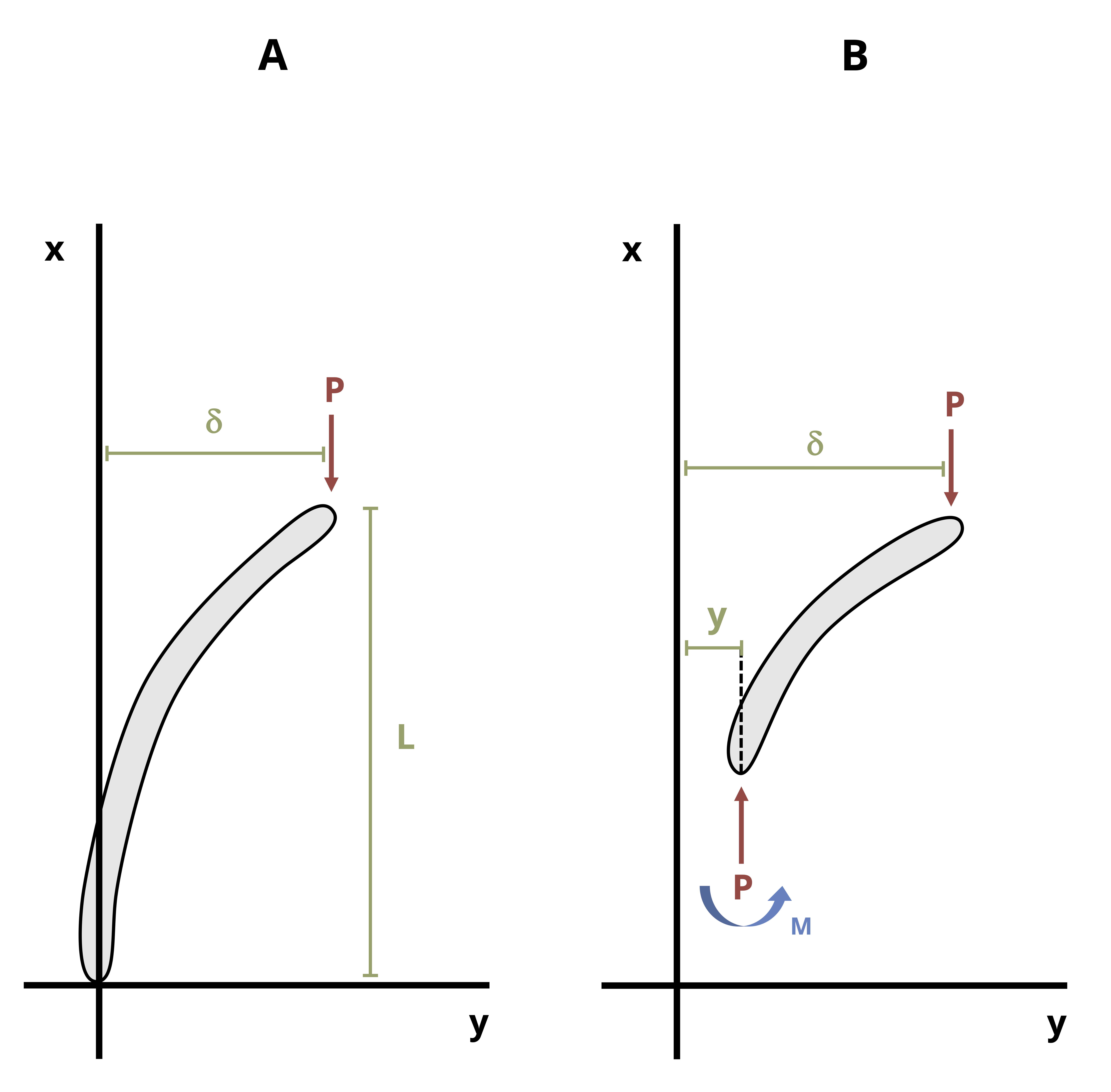
We can now write the differential equation using the elastic curve equation:
\[ \begin{aligned} & E I \frac{d^2 y}{d x^2}=P(\delta-y) \\ & \frac{d^2 y}{d x^2}+\left(\frac{P}{E I}\right) y=\left(\frac{P}{E I}\right) \delta \end{aligned} \]
Since the right side is not equal to zero, this equation is nonhomogeneous (note this differs from our earlier derivation for the pinned-pinned connection). There will be a particular and complementary solution.
\[ y=C_1 \sin \left(\sqrt{\frac{P}{E I} x}\right)+C_2 \cos \left(\sqrt{\frac{P}{E I} x}\right)+\delta \]
We can now employ boundary conditions to solve for the constants. At x = 0, y = 0, so C2 = δ. Also at x = 0, dy/dx=0, so C1=0. This leads us to the following deflection curve:
\[ y=\delta\left(1-\cos \left(\sqrt{\frac{P}{E I}} x\right)\right) \]
At the free end of the column, x = L, we know that y = δ so:
\[ 0=\delta \cos \left(\sqrt{\frac{P}{E I} L}\right) \]
The trivial solution δ = 0 shows that no matter what the P value no buckling will occur. So we have:
\[ \begin{aligned} & 0=\cos \left(\sqrt{\frac{P}{E I} L}\right) \\ & \sqrt{\frac{P}{E I}} L=\frac{n \pi}{2} \\ & \text{where n=1, 3, 5,...} \end{aligned} \]
The smallest critical load happens at n = 1, results in:
\[ P_{c r}=\frac{\pi^2 E I}{(2 L)^2} \]
Other support conditions can be derived in a similar manner.
15.2.1 Effective Length
The critical load equation for the fixed-free column differs from the equation for the pinned-pinned column only by the length L being multiplied by a factor of 2. We will adjust the column length L to denote the distance between the points on the column where the moment is zero. This distance is referred to as the effective length, Le. For a pinned-pinned column, L = Le, as illustrated in Figure 15.9. As derived above, for a column with a fixed base and a free end, Le = 2L. Two other common end conditions are depicted in this figure relating L to Le. We can use one general equation for any support condition by replacing the effective length with KL, where K represents the effective length factor.
\[ \boxed{P_{c r}=\frac{\pi^2 E I}{(K L)^2}} \tag{15.3}\]
and
\[ \boxed{\sigma_{c r}=\frac{\pi^2 E}{\left(\frac{K L}{r}\right)^2}} \tag{15.4}\]
You can find the effective length factor, K, below each of the end conditions in Figure 15.9.
Example 15.2 and Example 15.3 demonstrate how to calculate the critical buckling load in columns with various different supports.
Example 15.2
Redo Example 15.1 with a fixed-fixed column.
We will consult the table in Appendix A to get the section properties of a W10x30 section.
\[ \begin{aligned} & A=8.84{~in.}^2 \\ & I_x=170{~in.}^4 \\ & r_y=4.38{~in.} \\ & I_y=16.7{~in.}^4 \\ & r_y=1.37{~in.} \end{aligned} \]
We will start with calculating the critical load using Euler’s Bucking Formula. Note that we can confidently say that this column will buckle about the y-axis since the moment of inertia in the y-direction is the smallest.
\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I^2}{(k L)^2}=\frac{\pi^2(29000{~ksi})(16.7{~in.^4})}{\left(2*8{~ft}*12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=129.7{~kips} \\ & \end{aligned} \]
This represents the load at which any increase in applied load will cause the column to buckle. We will calculate the stress associated with this critical load.
\[ \sigma_{c r}=\frac{P_{cr}}{A}=\frac{129.7{~kips}}{8.84{~in.^2}}=14.7{~ksi} \]
Since this stress is smaller than the yield stress of the steel (σy = 50 ksi) the column will buckle first at a critical load of 129.7 kips.
Example 15.3
A W12x50 column carries a load of 650 kips. If the column is 25 feet long, has fixed-pinned end conditions, is braced at the midpoint in the weak direction, and is made from A492 steel (σy = 50 ksi and E = 29,000 ksi), is it adequate?
\[ \begin{aligned} & A=14.6{~in.}^2 \\ & I_x=391{~in.}^4 \\ & r_y=5.18{~in.} \\ & I_y=56.3{~in.}^4 \\ & r_y=1.96{~in.} \end{aligned} \]
We will consult the table in Appendix A to get the section properties of a W12x50 section. We will start with calculating the critical load using Euler’s Bucking Formula. The brace at the midpoint of the column changes the length of the column in the weak direction. This doesn’t make it obvious which axis the column will buckle about so we will need to check both the strong and weak directions.
Strong axis
\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I^2}{(k L)^2}=\frac{\pi^2(29000{~ksi})(391{~in.}^4)}{\left(0.7*25{~ft}*~12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=2,538{~kips} \\ & \end{aligned} \]
We use the general form of Euler’s bucking equation. Since the end supports are pinned-fixed, we use K = 0.7. We calculated that the critical load in the strong direction to be 2,538 kips.
We will compare this to buckling about the weak axis. The values of I, K, and L will change. The L value changes because the column is braced at the midpoint, so the column has a shorter distance to buckle about. The K value can be tricky. There were no details about the brace; we don’t know if the brace will provide an end condition like a fixed or pinned end. So, we will calculate the worst case, which would be a pinned-pinned end condition (this makes the denominator the largest, so the result will be the smallest).
Weak axis
\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I^2}{(k L)^2}=\frac{\pi^2(29000{~ksi})(56.3{~in.^4})}{\left(1*12.5{~ft}*12\frac{in.}{ft}\right)^2} \\ & P_{c r}=716{~kips} \\ \end{aligned} \]
We calculated that the critical load in the weak direction to be 716 kips. This means that if the column were to buckle, it would be about the weak axis since this load was smaller. Since the critical buckling load is greater than the 650 kip applied load our column is adequate. However, we also need to calculate the load that would cause yielding of the steel.
Yield
\[ \begin{aligned} \sigma_{yield}=\frac{P}{4} \quad\rightarrow\quad &P=(50{~ksi})(14.6{~in.^2}) \\ & P_{yield}=730{~kips} \end{aligned} \]
We calculated a yielding load of 730 kips. Interpreting these results: The column is adequate for a 650 kip load. Failure would first occur by bucking in the weak direction if the load were increased to 716 kips. It should be noted that we did not apply any safety factors. In civil engineering, design codes for steel columns designate how to apply safety factors to the loading and the capacity.
What would happen to the capacity of the columns if the brace was not there? We will recalculate the critical load for bucking bout the weak direction.
No brace
\[ \begin{aligned} & P_{cr}=\frac{\pi^2 E I^2}{(k L)^2}=\frac{\pi^2(29000{~ksi})(56.3{in.^4})}{\left(0.7*25{~ft}*12~\frac{in.}{ft}\right)^2} \\ & P_{c r}=365{~kips} \\ \end{aligned} \]
Notice how much lower this was than the braced condition. If the column was not braced it would not be adequate for the applied load.
Summary
Click to expand
References
Click to expand
Figures
Figure 15.1: Examples of columns. A: Unknown author. 2020. Pixabay license. https://pixabay.com/photos/bridge-tunnel-columns-structure-5441571/. B: ds_30. 2020. Pixabay license. https://pixabay.com/photos/buildings-concrete-construction-4839276/. C: G41rn8. 2009. CC BY-SA. https://commons.wikimedia.org/wiki/File:Hangzhou_2009_1794.jpg.
Figure 15.2: Buckling of a ruler. Amy Richardson. 2024. CC BY-NC-SA.
Figure 15.3: Free body diagram of a simplified column. Kindred Grey. 2024. CC BY-NC-SA.
Figure 15.4: Pinned-pinned axially loaded column. Kindred Grey. 2024. CC BY-NC-SA.
Figure 15.5: First three buckling modes. Kindred Grey. 2024. CC BY-NC-SA.
Figure 15.6: Buckling of wooden studs. scottnj. 2010. CC BY-NC-ND. https://flic.kr/p/8heJAn.
Figure 15.7: Plot of critical stress. Kindred Grey. 2024. CC BY-NC-SA.
Example 15.1: Kindred Grey. 2024. CC BY-NC-SA.
Figure 15.8: Column with a fixed base and a free end. Kindred Grey. 2024. CC BY-NC-SA.
Figure 15.9: Effective length of columns for various end conditions. Kindred Grey. 2024. CC BY-NC-SA.
Example 15.2: Kindred Grey. 2024. CC BY-NC-SA.
Example 15.3: Kindred Grey. 2024. CC BY-NC-SA.